L’essentiel du théorème de Pythagore : théorie et exemples
L’essentiel du théorème de Pythagore : théorie et exemples
C'est au philosophe et mathématicien grec Pythagore que nous devons le théorème éponyme, une pierre angulaire de la géométrie. En établissant la relation mathématique entre les trois côtés d'un triangle rectangle, Pythagore a ouvert la voie à une multitude d'applications pratiques. Son théorème est essentiel en architecture pour calculer les dimensions des structures, en navigation pour tracer des trajets optimaux, en physique pour résoudre des problèmes de mécanique, en musique pour comprendre les intervalles harmoniques, et bien plus encore. Pythagore a ainsi légué à l'humanité un outil mathématique précieux, dont l'utilité traverse les siècles et les disciplines.
Trouver un prof particulier de géométrie
Théorie :
Le théorème de Pythagore est un théorème qui permet de trouver la longueur d’un des côtés d’un triangle rectangle. Pour l’appliquer il faut impérativement savoir :
- Que le triangle concerné est rectangle
- La mesure de deux des côtés du triangle
Le théorème de Pythagore énonce :
Dans un triangle rectangle, l’hypoténuse au carré est égale à la somme des deux autres côtés au carré.
Il est ainsi possible d’écrire l’égalité de Pythagore, tel que :
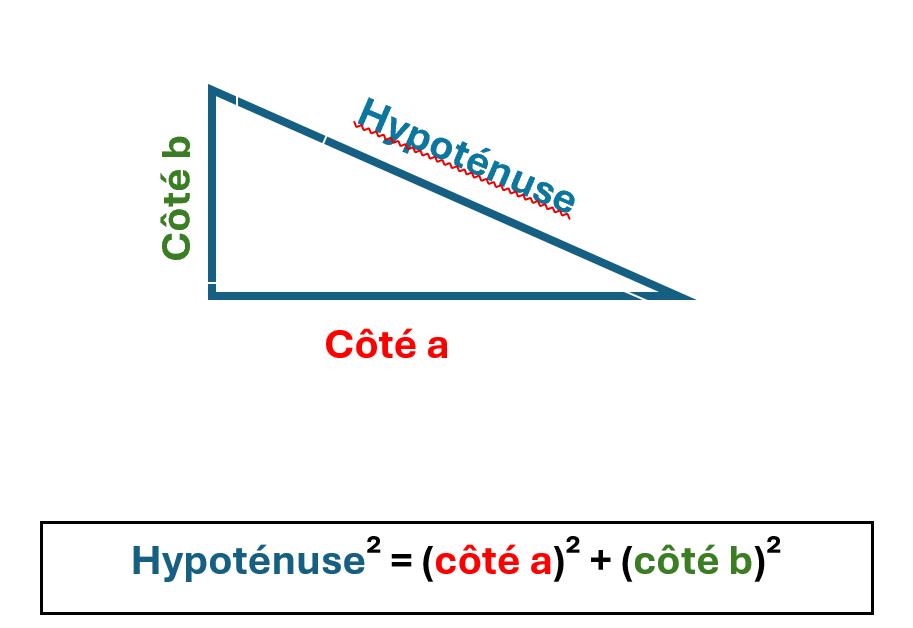
Rappel : l’hypoténuse est le côté d’un triangle rectangle qui se situe en face de l’angle droit
Méthode :
Voici les étapes à mettre en place afin d’utiliser correctement le théorème de Pythagore :
- Vérifier que le triangle est rectangle
- S’assurer que nous connaissons les longueurs de deux côtés du triangle
- Ecrire l’égalité de Pythagore en conservant l’ordre indiqué précédemment. ( l’hypoténuse est toujours « seule » de son côté de l’équation)
- Remplacer dans l’équation les leurs longueurs connues.
- Réduire et résoudre l’équation obtenue pour obtenir la longueur manquante
Exemple n° 1 : Recherche de l’hypoténuse
Dans le triangle ABC rectangle en B, le côté AB mesure 4cm et le côté BC mesure 3cm.
Nous allons à l’aide du théorème de Pythagore, calculer la longueur AC manquante.
Voici un exemple de rédaction :
Le triangle ABC est rectangle en B.
D’après le théorème de Pythagore :
AC² = AB² + BC²
AC² = 4² + 3²
AC² = 16 + 9
AC² = 25
AC = √25
AC = 5
La longueur AC mesure 5 cm.
Exemple n° 2 : Recherche d’un côté qui n’est pas l’hypoténuse
Dans le triangle IHJ rectangle en H, le côté IJ mesure cm et le côté HJ mesure cm.
Nous allons à l’aide du théorème de Pythagore, calculer la longueur IH manquante.
Voici un exemple de rédaction :
Le triangle IHJ est rectangle en H.
D’après le théorème de Pythagore :
IJ² = IH² + HJ²
10² = IH² + 5²
100 = IH² + 25
100 - 25 = IH²
75 = IH²
IH² = 75
IH = √75 (valeur exacte)
IH ~ 8,7 ( valeur arrondie au dixième)
La longueur IH mesure √75 cm, soit environ 8,7cm.
À toi de jouer maintenant !
Voici un exercice supplémentaire pour mettre en application ce que nous venons d'étudier :
Un agriculteur possède un terrain rectangulaire de 60 mètres de longueur et 40 mètres de largeur. Il souhaite construire une clôture le long des bords de ce terrain pour délimiter sa propriété. Pour économiser sur les matériaux, il souhaite placer une diagonale à travers le terrain. Utilisez le théorème de Pythagore pour déterminer la longueur de cette diagonale

